3. Integrationsverfahren
3.1. Rechteckverfahren
Mit dem Rechteckverfahren versucht man eine Funktion 
in
einem Intervall 
näherungsweise
durch das addieren von Rechteckflächen zu integrieren. Demzufolge zerlegt man
die Fläche durch Parallelen zur y-Achse und ersetzt den krummlinigen Teil durch
zur x-Achse parallele Strecken, so dass diese Parallelen gleichgroße Rechtecke
ergeben.5
Grundsätzlich hat man bei diesem Verfahren zwei Möglichkeiten um Integrale Näherungsweise
zu berechnen: Man kann entweder mit der Ober- oder Untersumme arbeiten. Aus gründen
der Einfachheit erkläre ich zuerst die Untersumme (
).
Anschließend werde ich kurz auf die Unterschiede zur Obersumme (
)
eingehen.
, der Abszissenachse (x-Achse) und den beiden Ordinaten 
und 
begrenzt wird. Man zerlegt die Fläche in eine Anzahl Rechtecke (siehe Abb. 1).
Die Summe dieser Recheckflächen ist kleiner als die gesuchte Fläche6 (Näherungswert).
Als erstes Teile ich die Fläche in 
-Rechtecke
ein, wobei diese Rechtecke immer die gleiche Breite 
haben.
Jetzt hat man die Breite jeder einzelnen Rechteckfläche. Mit der Breite erhält
man auch die Stützstellen 
der einzelnen Rechtecke.
Stützstellen. Stützstellen sind die Punke, an denen die Eckpunkte
der Rechtecke die x-Achse berühren. Dies kann man auch als Funktion darstellen.
Diese Funktion erhält man folgendermaßen: Die erste Stützstelle 
stellt
zugleich auch die äußerst linke Seite des Intervalls dar. Also ist 
!
Demnach lautet die nächste Stützstelle 
.
Wie unter Punkt 2 erwähnt stellt die
Strecke zwischen zwei Stützstellen oder die Breite eines Rechteckes dar. Also
kann man jede weitere Stützstelle berechnen, indem man zu der 1. Stützstelle
entsprechend viele hinzuaddiert.
Spielt man dies nun weiter, so kommt man so auch zur letzten Stützstelle. Die
letzte Stützstelle ist der letzte Eckpunkt eines Rechteckes vor dem Intervallende.
Für das Intervallende kann man auch 
schreiben,
also gilt für die letzte Stützstelle 
!
Daraus folgt, dass sich jede Stützstelle wie folgt berechnen lässt, wobei 
hier
für die zu berechnende Rechteckfläche steht:
den
entsprechenden Funktionswert 
berechnet.
Also errechnet sich die Fläche eines Rechteckes wie folgt: 
.
Einfach ausgedrückt: Höhe x Breite!
Die Summe 
ergibt
den Näherungswert der zu berechnenden Fläche.
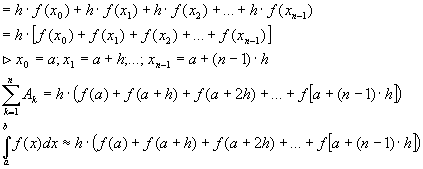
Rechteckregel (Untersumme)8
Beispiel: Integriert man die Funktion 
im
Intervall 
, so erhält man bei 
für
die Untersumme folgendes Ergebnis:
Das genaue Integral beträgt 
.
Vergleicht man diese Ergebnisse, so erkennt man, dass das Ergebnis der
Untersumme unter dem genauen Integral liegt.
Unterschiede zwischen Ober- und Untersumme
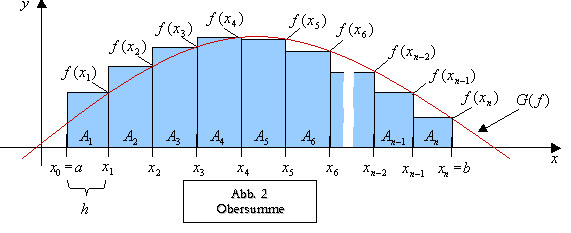
Die Berechnung der Obersumme erfolgt im wesendlichen genauso wie bei der Untersumme. Ein Unterschied liegt darin, dass die Summe der
Recheckflächen größer ist als die gesuchte Fläche (siehe Abb. 2). Des weiteren ist die 1. Stützstelle
nicht mehr ,
sondern und
die letzte Stützstelle ist gleich dem Intervallende .
Demnach ändert sich die Formel für 
wie folgt:
Rechteckregel (Obersumme)
Diese Regel sei hier noch mal graphisch Dargestellt:
Beispiel: Integriert man die Funktion
im Intervall , so erhält man bei
für die Obersumme folgendes Ergebnis:
Das genaue Integral beträgt
. Vergleicht man diese Ergebnisse, so erkennt man, dass das Ergebnis der Obersumme über dem genauen Integral liegt.
=> Wenn man die Ergebnisse von Ober- und Untersumme vergleicht und 
eine
monotone Funktion ist, so stellt man fest, dass der genaue Integralwert
zwischen diesen beiden Summen liegt!
