3.2 Trapezverfahren

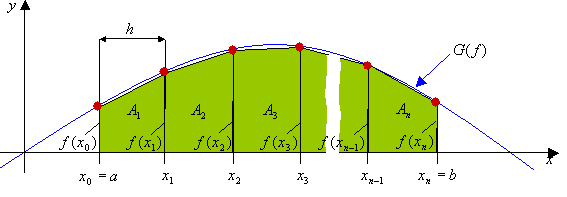
Mit diesem Verfahren versucht man eine Funktion in einem Intervall näherungsweise durch die Addition von gleich breiten Trapezflächen parallel zur y-Achse zu integrieren.⁹ 

Zuerst unterteilt man das Intervall in Teile der Breite . Um nun für jedes Teil die gleiche Breite zu bekommen, ermittelt man zuerst die Gesamtbreite des Intervalls und teilt diese durch die Anzahl der Teile, die man verwenden möchte. Durch diese Unterteilung des Intervalls erhält man die Stützstellen . An diesen Stützstellen

berechnet man nun die zugehörigen Funktionswerte .¹⁰ Nun hat man die einzelnen Flächen der Trapeze. Um jetzt die Flächenmaßzahl zu erhalten muss man nur noch die einzelnen Flächen miteinander addieren:

.

Berechnung der Fläche eines Trapezes

Mit dem Term wird die Fläche eines der Trapeze berechnet. Da die Berechnung von bereits bekannt ist, benötigt man zur Flächenberechnung jetzt noch die Höhe. Generell wird die Höhe eines Trapezes wie folgt berechnet: ¹¹ oder wie hier . Die Parameter und stellen jeweils die Seiten des Trapezes dar und können hier durch die Funktionswerte ersetz werden.

¹² 

Die Formel für die Summe der Maßzahlen aller Trapezflächen heißt Trapezregel und ergibt einen Näherungswert für den gesuchten Integralwert .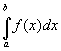

Zusammenhang von Rechteckregel und Trapezregel:

Vergleicht man die Formel für die Trapezregel mit der Formel für die Rechteckregel, so erhält man eine einfache Beziehung zwischen diesen beiden Regeln.¹³ 

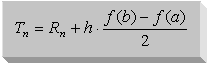
Trapezregel¹⁴