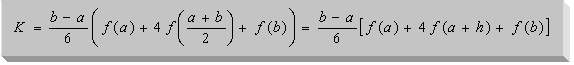Johannes
Kepler wurde am 27.12.1571 in Weil geboren. Zu Lebzeiten war er als Astronom und
Mathematiker tätig. Kepler stammte aus bescheidenen Verhältnissen. 1583
legte er das „Landexamen“ ab, was ihm die Berechtigung verschaffte, ein
Theologiestudium als Stipendiat zu absolvieren. Er besuchte 1584 die
Klosterschule in Adelberg und 1586 in Maulbronn und bezog 1589 die Universität Tübingen, um dort ev. Theologie zu
studieren. Sein wichtigster Lehrer war der Mathematiker und Astronom Michael
Maestlin (Geb. 1550, gest. 1631), der ihn mit dem kopernikanischem Weltbild
vertraut machte. 1594 ging Kepler als „Lehrer der Mathematik und Moral“ an
die ev. Stiftschule nach Granz. Zugleich wurde er Mathematiker der
Landesregierung und erstellte in dieser Eigenschaft Kalender. 1600 wurde er mit
seiner Familie aus Granz vertrieben (Gegenreformation) und siedelte nach Prag über,
wo er später (um 1601) kaiserlicher Mathematiker Rudolfs II. wurde. Keplers wichtigster Beitrag zur
Mathematik ist die „Nova stereometria
doliorum vinariorum“ („Neue Stereometrie der Fässer“) aus dem Jahre
1615, in der er Flächen und Volumen mit Hilfe von Indivisiblilien berechnete (Keplersche
Fassregel). Weitere Werke Keplers sind die Keplerschen Gesetze und andere.
Johannes Kepler verstarb am 15.11.1630 in Regensburg28
3.4.2 Die Keplersche Fassregel
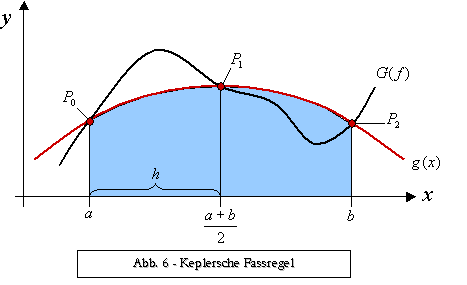
Ziel der Keplerschen Fassregel ist es, mit wenig Aufwand
eine krummlinig begrenzte Fläche 
im
Intervall 
zu Berechnen. Dazu soll diese Funktion durch eine Parabel 
ersetzt werden, die den Funktionsgraphen 
an drei Stellen 
berührt.29
Um die Fläche dieser Parabel im Intervall
zu berechnen, bilden wir zunächst die Aufleitung. Anschließend wird
diese Aufleitung so weit wie möglich umgeformt:
30
ausklammern!
ausklammern!
Klammern auflösen!
Rein rechnerisch kann man nun zunächst nichts mehr machen.
Da diese Formel jedoch immer noch zu aufwendig ist (der Parameter 
ist nicht bekannt), versuchen wir nun diese Formel soweit abzuändern, dass dennoch das oben genannte Ziel erreicht wird.
Ein Funktionswert der Parabel ergibt sich aus dem Term
. Für die Keplersche Fassregel werden 3 Funktionswerte (
oder )
benötigt. Diese 3 Punkte ()
sind in der eckigen Klammer enthalten. Also liegt es nahe, den Inhalt der
Klammer so umzuordnen, dass die benötigten Funktionswerte leicht abzulesen
sind. Da wir wissen, das der 1. Funktionswert vom Parameter 
abhängig ist und der 3. vom Parameter 
muss der 2. folglich von beiden
Parametern abhängig sein.
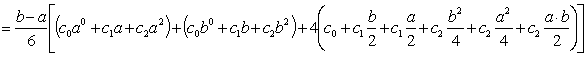
Da die Funktionswerte von 
an
den Stellen 
,
und
sein sollen, lautet die Keplersche Fassregel
wie folgt:
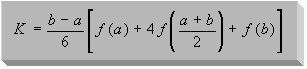
Keplersche Fassregel32
Außer dieser Herleitung gibt es noch andere Methoden, um
die Keplersche Fassregel herzuleiten. Wenn man z. B. bei der Simpsonregel
(siehe Punkt 3.3.3!) für 
einsetzt,
so gelangt man ebenfalls zu dieser Regel:
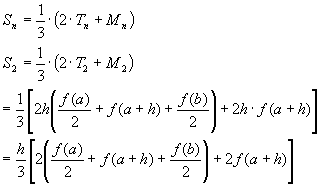
, da hier bei der Keplerschen Fassregel die Fläche in 2 Teile Aufgeteilt wird
Vergleicht man dieses Ergebnis nun mit der Keplerschen Fassregel, so sieht man, dass sie identisch sind!
