Thomas Simpson wurde am 20.08.1710 in Market Bosworth in England geboren. Obwohl er ursprünglich Weber war, wurde sein Interesse an Mathematik durch ein Selbststudium geweckt. Er war ab 1743 Professor an der Militärakademie in Woolwich. In seinem Leben verfasste er mehrere Lehrbücher. Darunter u. a. über Algebra, Geometrie und I. Newtons Fluxionsrechnung. Er verstarb 14.05.1761.15
3.3.2 Die Mittentangentenregel
Diese Regel wird für die Herleitung der Simpsonregel verwendet. Dies ist jedoch nur eine Möglichkeit, die Simpsonregel herzuleiten. Eine andere besteht in der Verwendung der Keplerschen Fassregel. Ich habe mich jedoch für die Mittentangentenregel entschieden, weil ich sie mir selber leichter verständlich machen konnte.
Ähnlich wie beim Trapezverfahrens soll hier eine krummlinig begrenzte Fläche im Intervall 
näherungsweise
durch Addition von gleich breiten Trapezflächen parallel zur y-Achse berechnet werden. Jedoch soll hier eine Trapezseite jeweils an jeder zweiten Stützstelle
Tangente des Funktionsgraphen sein.16
in 
Teile
der gleichen Breite 
wobei
hier für eine gerade natürliche Zahl stehen soll. Anschließend zeichnet man
an jeder Stützstelle mit ungeradem Index (
)
eine Tangente an den Graphen.17 Die Enden der Tangente liegen jeweils an der Stützstelle
vor und nach dieser Stützstelle. Hierdurch erhält man Trapeze, die ein wenig
über den Funktionsgraphen hinausgehen (siehe Abb. 4) Daraus kann man ersehn,
dass die Mittentangentenregel sehr
ungenau ist, obwohl sie zum großen Teil auf dem Trapezverfahren beruht.
Diese Ungenauigkeit beruht auch darauf, das die Fläche dieser Trapeze nicht
mehr mit 
,
sondern mit 
berechnet wird. Die Breite dieser Flächen beträgt, wie in der oberen
Zeichnung zu sehen ist 
,
da eine Seite der Fläche immer über eine Stützstelle (über 
)
hinausgeht. Die Funktionswerte werden jeweils an der Stützstelle berechnet, bei
dem der Index ungerade ist. Es macht
hier also keinen Sinn, den Funktionswert an jeder Stützstelle zu berechnen,
weil man damit nicht die Eckpunkte des Trapezes berechnen kann. Dies ist auch
der Grund, warum man die Fläche 
nicht
mit 
berechnen kann.
Addiert man hier jetzt die Flächen aller Trapeze, so erhält man den Näherungswert 
Mittentangentenregel18
3.3.3 Simpsonregel unter Verwendung der Mittentangentenregel und des Trapezverfahrens
Gegeben sei die Funktion 
.
Berechnet man das Integral im Intervall 
durch
den gemeinsamen Grenzwert von Ober- und Untersumme, so erhält man als Ergebnis:
Nun soll dieser Wert mit den Ergebnissen aus der Anwendung der Trapezregel und der Mittentangentenregel verglichen werden, wobei die Fläche immer in 10 gleichgroße Teile zerlegt werden soll.
Anmerkung: Für beide Regeln gilt 
Ergebnis der Trapezregel:
Ergebnis der Mittentangentenregel:
Vergleicht man nun die beiden Ergebnisse mit dem genauen Integral, so stellt man fest, das die Trapezregel um ungef. 0,00295 (0,27%) und die Mittentangentenregel um ungef. 0,005755 (0,53%) abweicht.23
Auch fällt auf, dass das Ergebnis der Trapezregel über und das Ergebnis der Mittentangentenregel
unter dem Wert der Flächenmaßzahl liegt. Es währe daher interessant, herauszufinden, ob das arithmetische
Mittel 
beider Regeln ein genaueres Ergebnis bringt. Um das vermutete Ergebnis noch zu
verfeinern, sollte die Trapezregel mit einer doppelten Gewichtung in den Mittelwert eingehen, da sie doppelt so genau ist
wie die Mittentangentenregel.24
Diese Regel wird auch als Simpsonische Regel bezeichnet.
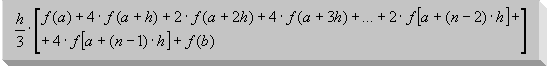
Simpsonische Regel26
Vergleicht man nun das Ergebnis der Simpsonischen Regel mit den beiden vorherigen, so erhält man ein viel genaueres Ergebnis:
=1,089699
Die Abweichung vom genauen Integral beträgt hier nur noch 0,008%! Eine andere Möglichkeit, um zur Simpsonischen Regel zu gelangen, liegt in der mehrmaligen Anwendung der Keplerschen Fassregel (3.4.2).27
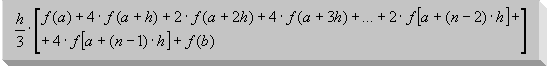
Simpsonische Regel
Wenn man nun diese beiden Regeln miteinander vergleicht, so stellt man fest, dass beide miteinander identisch sind! Man arbeitet also bei der Simpsonischen Regel auch mit Parabeln!
Anwendung:
Zunächst unterteilt man das Intervall in -Teile
der gleichen Breite. Eine Parabel (höchstens
2. Grades!) soll hier genauso wie bei der Keplerschen Fassregel den
Funktionsgraphen an drei Stellen (
)
berühren, die jeweils über den Stützstellen 
liegen.
Das heißt, das die Schnittpunkte von Parabel und Funktionsgraph immer über
den Stützstellen liegen. Eine direkt unterm Scheitelpunkt, und die anderen
jeweils links und rechts davon. Die Strecke zwischen der linken und der
rechten Stützstelle beträgt jeweils .
Zur Veranschaulichung sei dies hier noch mal in einer Zeichnung dargestellt:
